Publications

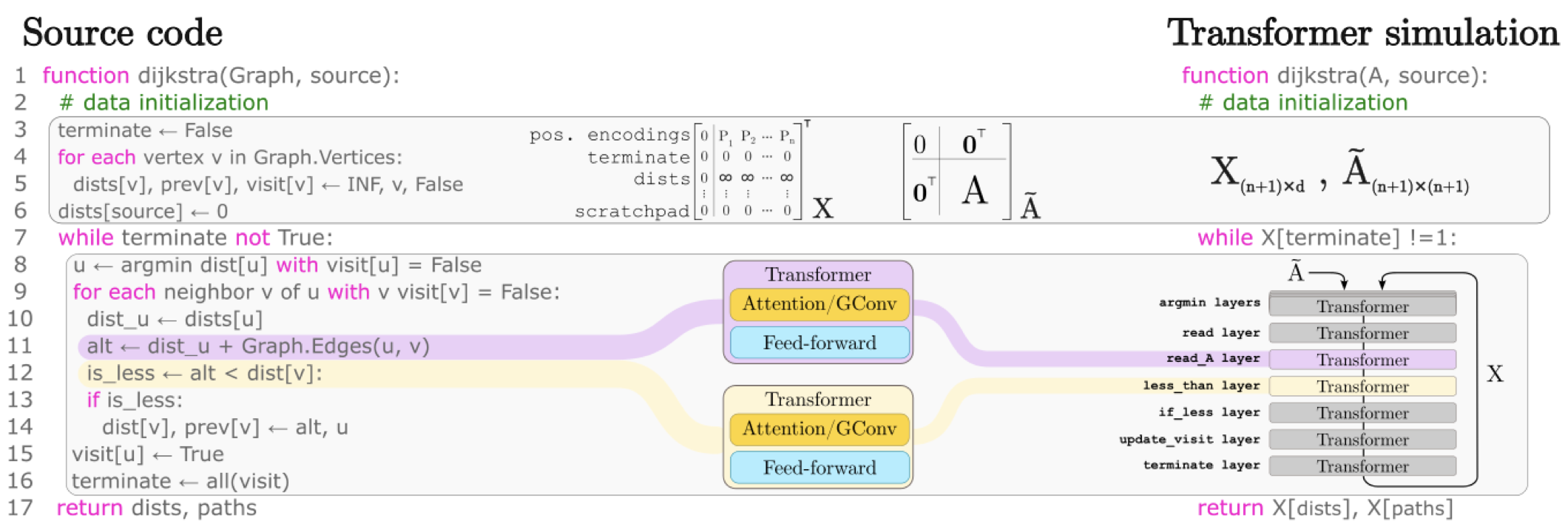
The execution of graph algorithms using neural networks has recently attracted significant interest due to promising empirical progress. This motivates further understanding of how neural networks can replicate reasoning steps with relational data. In this work, we study the ability of transformer networks to simulate algorithms on graphs from a theoretical perspective. The architecture that we utilize is a looped transformer with extra attention heads that interact with the graph. We prove by construction that this architecture can simulate algorithms such as Dijkstra’s shortest path algorithm, Breadth- and Depth-First Search, and Kosaraju’s strongly connected components algorithm. The width of the network does not increase with the size of the input graph, which implies that the network can simulate the above algorithms for any graph. Despite this property, we show that there is a limit to simulation in our solution due to finite precision. Finally, we show a Turing Completeness result with constant width when the extra attention heads are utilized.

A. Back de Luca, K. Fountoulakis

arXiv:2402.01107

(Preprint)

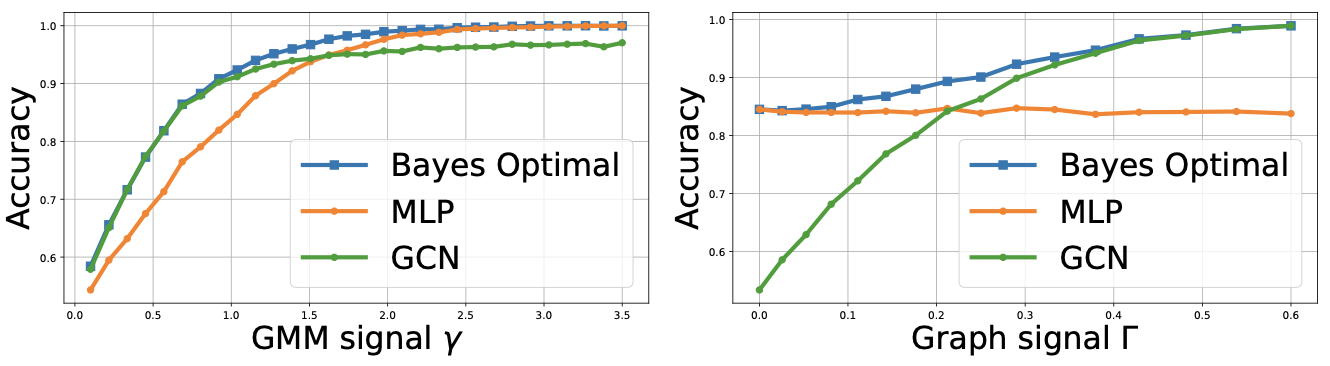
We study the node classification problem on feature-decorated graphs in the sparse setting, i.e., when the expected degree of a node is O(1) in the number of nodes. Such graphs are typically known to be locally tree-like. We introduce a notion of Bayes optimality for node classification tasks, called asymptotic local Bayes optimality, and compute the optimal classifier according to this criterion for a fairly general statistical data model with arbitrary distributions of the node features and edge connectivity. The optimal classifier is implementable using a message-passing graph neural network architecture. We then compute the generalization error of this classifier and compare its performance against existing learning methods theoretically on a well-studied statistical model with naturally identifiable signal-to-noise ratios (SNRs) in the data. We find that the optimal message-passing architecture interpolates between a standard MLP in the regime of low graph signal and a typical convolution in the regime of high graph signal. Furthermore, we prove a corresponding non-asymptotic result.

A. Baranwal, K. Fountoulakis, A. Jagannath

arXiv:2305.10391 (accepted at NeurIPS 2023)

(Preprint)

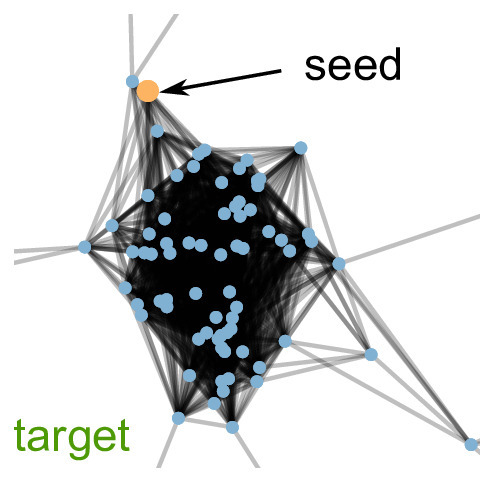
Local graph clustering methods aim to detect small clusters in very large graphs without the need to process the whole graph. They are fundamental and scalable tools for a wide range of tasks such as local community detection, node ranking and node embedding. While prior work on local graph clustering mainly focuses on graphs without node attributes, modern real-world graph datasets typically come with node attributes that provide valuable additional information. We present a simple local graph clustering algorithm for graphs with node attributes, based on the idea of diffusing mass locally in the graph while accounting for both structural and attribute proximities. Using high-dimensional concentration results, we provide statistical guarantees on the performance of the algorithm for the recovery of a target cluster with a single seed node. We give conditions under which a target cluster generated from a fairly general contextual random graph model, which includes both the stochastic block model and the planted cluster model as special cases, can be fully recovered with bounded false positives. Empirically, we validate all theoretical claims using synthetic data, and we show that incorporating node attributes leads to superior local clustering performances using real-world graph datasets.

S. Yang, K. Fountoulakis

International Conference on Machine Learning (ICML) 2023, Oral

(Preprint) (Code) (Video)

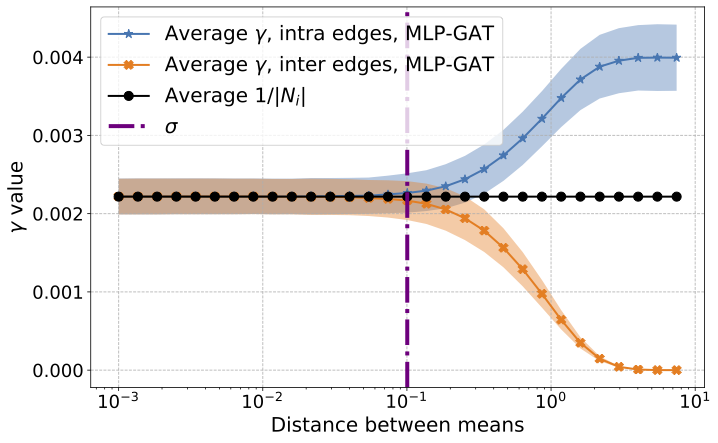
Graph-based learning is a rapidly growing sub-field of machine learning with applications in social networks, citation networks, and bioinformatics. One of the most popular type of models is graph attention networks. These models were introduced to allow a node to aggregate information from the features of neighbor nodes in a non-uniform way in contrast to simple graph convolution which does not distinguish the neighbors of a node. In this paper, we study theoretically this expected behaviour of graph attention networks. We prove multiple results on the performance of the graph attention mechanism for the problem of node classification for a contextual stochastic block model. Here the features of the nodes are obtained from a mixture of Gaussians and the edges from a stochastic block model where the features and the edges are coupled in a natural way. First, we show that in an “easy” regime, where the distance between the means of the Gaussians is large enough, graph attention maintains the weights of intra-class edges and significantly reduces the weights of the inter-class edges. As a corollary, we show that this implies perfect node classification independent of the weights of inter-class edges. However, a classical argument shows that in the “easy” regime, the graph is not needed at all to classify the data with high probability. In the “hard” regime, we show that every attention mechanism fails to distinguish intra-class from inter-class edges. We evaluate our theoretical results on synthetic and real-world data.

K. Fountoulakis, A. Levi, S. Yang, A. Baranwal, A. Jagannath

Journal of Machine Learning Resarch

(Preprint) (Code) (Video)

Best paper award at the GroundedML workshop at ICLR 2022.